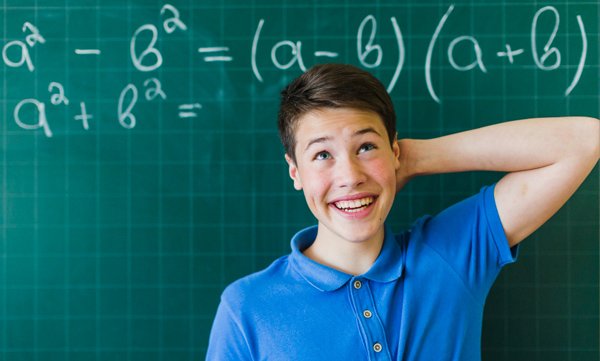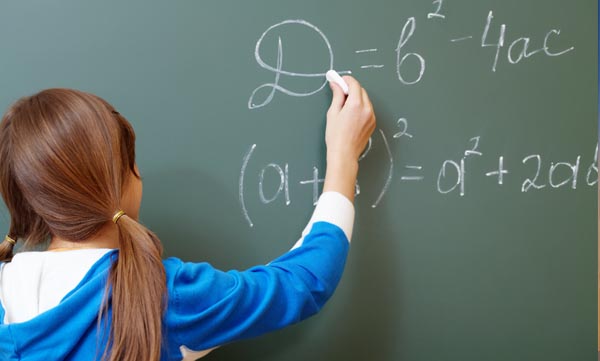What is Algebra
Algebra is a branch of maths that substitutes letters for numbers. An algebraic equation depicts a scale, what is done on one side of the scale with a number is also done on either side of the scale. Mathematical numbers are constants. Algebra also includes real numbers, complex numbers, matrices, vectors, and much more. X, Y, A, and B are the most commonly used letters that represent algebraic problems and equations.
Algebra Formula for Kids
Algebra Formulas form the foundation of numerous most important topics of mathematics. Topics like equations, quadratic equations, polynomials, coordinate geometry, calculus, trigonometry, and probability, extensively depend on algebra formulas for understanding and for solving complex problems.
Algebra formula for kids
Basics of Algebra cover the simple operation of mathematics like addition, subtraction, multiplication, and division involving both constants as well as variables. For example, x+10 = 0. This introduces an important algebraic concept known as equations. The algebraic equation can be thought of as a scale where the weights are balanced through numbers or constants.
Algebra is the branch of Maths that uses alphabetical letters to find unknown numbers. These letters are also called variables. The values that are known in the given expression such as numbers are called constants. However in higher classes, students will learn the concept of algebra at the potential level. But when we speak about its basics, it covers the general algebraic expressions, formulas, and identities, which are used to solve many mathematical problems. Let us learn here the basic concept of algebra with the help of some terminology, formulas, rules, examples, and solved problems.
In the above-given equation, the letters a and b are the unknown variables that we have to determine. Whereas c denotes the constant term.
Learn More:
Algebra Formula Definition
The Algebra formula is part of Class 10 in India. One of the most crucial areas of mathematics is algebra. Numerous disciplines, including quadratic equations, polynomials, coordinate geometry, calculus, trigonometry, probability, and others, can be solved using algebraic formulas. In Algebra formulas, we used numbers along with letters together. The most common letters used in algebraic equations and problems are X, Y, A, and B. These Algebra formulas enable us to quickly and efficiently tackle time-consuming algebraic problems. Here, we include all significant Algebra formulas together with their solutions, so that students can access them all in one place.
For Algebra formulas Example,
(a+b)³ =a³+ 3a²b+3ab²+b³
In the above Algebra formulas, both sides are individually an algebraic equation. Where ( a³ + 3a²b+3ab²+b³ ) is the simplified expression of (a+b)³
Basic Algebra
The algebra for class 6 covers all the basic concepts. Terms related to basic algebra skills are mentioned below.
- Exponent
- Expression
- Polynomial (Monomial, binomial and trinomial)
- Like terms and Unlike terms
- Constants
An equation is a statement that implies two same identities separated by “=” sign. Whereas an expression is a group of different terms separated by ‘+’ or ‘-‘ sign.
Like terms are those terms whose variables and their exponents are same.
Basic Algebra Rules
The basic algebra rules are mentioned below:
- The Symmetry rule
- The commutative rules
- The inverse of adding
- Two rules for equation
Basic Algebra Operations
The general arithmetic operations performed in the case of algebra are:
Addition: x + y
Subtraction: x – y
Multiplication: xy
Division: x/y or x ÷ y
where x and y are the variables.
The order of these operations will follow the BODMAS rule, which means the terms inside the brackets are considered first. Then, roots and exponents are operated on second priority. Solve all the division and multiplication operations and later addition and subtraction.
Algebra Formulas Identities
In algebra formulas, an identity is an equation that is always fall true regardless of the values assigned to the variables. Algebraic Identity means that the equation’s left-hand side (LHS) is identical to the right-hand side (RHS) of the equation and for all values of the variables. Algebraic identities applications are in solving the values of unknown variables. Here are some commonly used algebraic identities:
Definition of Algebraic identities:
Algebraic identities are equations that hold true for all possible values of variables. Numbers, variables (unknown values), and mathematical operators make up algebraic identities and expressions (addition, subtraction, multiplication, division, etc.) Algebraic identities are utilized in a variety of mathematical fields, including algebra, geometry, and trigonometry. These are mostly used to find the factors of a polynomial. A deeper understanding of algebraic identities helps to improve the efficiency with which problem sums are solved. The factorization of polynomials is among the most important applications of algebraic identities.
Everything About Algebraic Identities:
An identifier is an equation that holds true for all values of the variables in it. For all variable values, an algebraic identifier is an equation in which the value of the left-hand side of the equation equals the value of the right-hand side of the equation. In different disciplines of mathematics, we have several standard identifiers that we might use. The Binomial assertion yields all standard Identities. An algebraic identifier is an algebraic equation that refers to all of the values of a variable in it. It is also employed in the factoring of polynomials. As a result, algebraic identifiers are utilized to calculate algebraic expressions and solve various polynomials. In your younger classes, you must have learned about Algebraic Identities. You will review those ideas and improve your learning in this lesson.
How to verify algebraic identity?
The method of substitution is used to check that the algebraic identities are true. Substitute values for the variables and conduct the arithmetic operation with this method. The activity technique is another way to check the algebraic identity. You’ll need a basic understanding of geometry for this procedure, as well as certain materials to prove your identity.
What’s the difference between identities and algebraic expressions?
An algebraic expression is an expression that has both a variable and a constant. A variable in an expression can have any value. As a result, if the variable values change, the expression value can change. However, algebraic identity is equality that holds for all variables’ values.
Here, we will provide a list of all the important algebra formulas. The comprehensive list will allow the students to have a quick look before exams or refer to it whenever they wish. Remember, only rote learning is not enough. You must also know how to effectively apply these formulas to a problem.
All algebra formula,
- a² – b² = (a-b)(a+b)
- (a+b)² = a² + 2ab + b²
- (a-b)² = a² – 2ab + b²
- a² + b² = (a-b)² +2ab
- (a+b+c)² = a²+b²+c²+2ab+2ac+2bc
- (a-b-c)² = a²+b²+c²-2ab-2ac+2bc
- a³-b³ = (a-b) (a² + ab + b²)
- a³+b³ = (a+b) (a² – ab + b²)
- (a+b)³ = a³+ 3a²b + 3ab² + b³
- (a-b)³ = a³- 3a²b + 3ab² – b³
- “n” is a natural number, an – bn = (a-b) (an-1 + an-2b +….bn-2a + bn-1)
- “n” is a even number, an + bn = (a+b) (an-1 – an-2b +….+ bn-2a – bn-1)
- “n” is an odd number an + bn = (a-b) (an-1 – an-2b +…. – bn-2a + bn-1)
- (am)(an) = am+n (ab)m = amn
Conclusion:
An algebraic expression or equation is just a mathematical expression. Constants, variables, and exponents make the method an algebraic equation. If the value of the variable changes and the equilibrium is not satisfied, the equation cannot be called an equation. Students benefit from knowledge and understanding of these symbols as they learn statistical methods. It can also improve their skills in applying these techniques to algebraic manipulation and problem-solving.